Глава 7.1. По-сложни цикли
След като научихме какво представляват и за какво служат for циклите, сега предстои да се запознаем с други видове цикли, както и с някои по-сложни конструкции за цикъл. Те ще разширят познанията ни и ще ни помагат в решаването на по-трудни и по-предизвикателни задачи. По-конкретно, ще разгледаме как се ползват следните програмни конструкции:
- цикли със стъпка
whileциклиdo-whileцикли- безкрайни цикли
В настоящата тема ще разберем и какво представлява операторът break, както и как чрез него да прекъснем един цикъл. Също така, използвайки try-catch конструкцията, ще се научим да следим за грешки по време на изпълнението на програмата ни.
Видео
Цикли със стъпка
В главата "Повторения (цикли)" научихме как работи for цикълът и вече знаем кога и с каква цел да го използваме. В тази тема ще обърнем внимание на една определена и много важна част от конструкцията му, а именно стъпката.
Какво представлява стъпката?
Стъпката е тази част от конструкцията на for цикъла, която указва с колко да се увеличи или намали стойността на водещата му променлива. Тя се декларира последна в скелета на for цикъла.
Най-често е с размер 1 и в такъв случай, вместо да пишем i += 1 или i -= 1, можем да използваме операторите
i++ или i--. Ако искаме стъпката ни да е различна от 1, при увеличение използваме оператора i += (размера на стъпката), а при намаляване i -= (размера на стъпката). При стъпка 10, цикълът би изглеждал по следния начин:
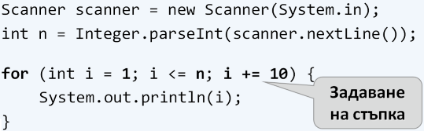
Следва поредица от примерни задачи, решението на които ще ни помогне да разберем по-добре употребата на стъпката във for цикъл.
Пример: числата от 1 до N през 3
Да се напише програма, която отпечатва числата от 1 до n със стъпка 3. Например, ако n = 100, то резултатът ще е: 1, 4, 7, 10, …, 94, 97, 100.
Можем да решим задачата чрез следната поредица от действия (алгоритъм):
- Четем числото
nот входа на конзолата. - Изпълняваме
forцикъл от 1 доnс размер на стъпката 3. - В тялото на цикъла отпечатваме стойността на текущата стъпка.

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#0.
Пример: числата от N до 1 в обратен ред
Да се напише програма, която отпечатва числата от n до 1 в обратен ред (стъпка -1). Например, ако n = 100, то резултатът ще е: 100, 99, 98, …, 3, 2, 1.
Можем да решим задачата по следния начин:
- Четем числото
nот входа на конзолата. - Създаваме
forцикъл, като присвоявамеint i = n. - Обръщаме условието на цикъла:
i >= 1. - Дефинираме размера на стъпката: -1.
- В тялото на цикъла отпечатваме стойността на текущата стъпка.

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#1.
Пример: числата от 1 до 2^n с for цикъл
В следващия пример ще разгледаме ползването на обичайната стъпка с размер 1, но с малко по-различна логика в тялото на цикъла.
Да се напише програма, която отпечатва числата от 1 до 2^n (две на степен n). Например, ако n = 10, то резултатът ще е 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024.

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#2.
Пример: четни степени на 2
Да се отпечатат четните степени на 2 до 2^n: 2^0, 2^2, 2^4, 2^8, …, 2^n. Например, ако n = 10, то резултатът ще е 1, 4, 16, 64, 256, 1024.
Ето една идея как можем да решим задачата:
- Създаваме променлива
numза текущото число, на която присвояваме начална стойност 1. - За стъпка на цикъла задаваме стойност 2.
- В тялото на цикъла: отпечатваме стойността на текущото число и увеличаваме текущото число
num4 пъти (според условието на задачата).

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#3.
While цикъл
Следващият вид цикли, с които ще се запознаем, се наричат while цикли. Специфичното при тях е, че повтарят блок от команди, докато дадено условие е истина. Като структура се различават от тази на for циклите, даже имат опростен синтаксис.
Какво представлява while цикълът?
В програмирането while цикълът се използва, когато искаме да повтаряме извършването на определена логика, докато е в сила дадено условие. Под "условие", разбираме всеки израз, който връща true или false. Когато условието стане грешно, while цикълът прекъсва изпълнението си и програмата продължава с изпълнението на останалия код след цикъла. Конструкцията за while цикъл изглежда по този начин:

Следва поредица от примерни задачи, решението на които ще ни помогне да разберем по-добре употребата на while цикъла.
Пример: редица числа 2k+1
Да се напише програма, която отпечатва всички числа ≤ n от редицата: 1, 3, 7, 15, 31, …, като приемем, че всяко следващо число = предишно число * 2 + 1.
Ето как можем да решим задачата:
- Създаваме променлива
numза текущото число, на която присвояваме начална стойност 1. - За условие на цикъла слагаме текущото число <= n.
- В тялото на цикъла: oтпечатваме стойността на текущото число и увеличаваме текущото число, използвайки формулата от условието на задачата.
Ето и примерна реализация на описаната идея:

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#4.
Пример: число в диапазона [1 … 100]
Да се въведе цяло число в диапазона [1 … 100]. Ако въведеното число е невалидно, да се въведе отново. В случая, за невалидно число ще считаме всяко такова, което не е в зададения диапазон.
За да решим задачата, можем да използваме следния алгоритъм:
- Създаваме променлива
num, на която присвояваме целочислената стойност, получена от входа на конзолата. - За условие на цикъла слагаме израз, който е
true, ако числото от входа не е в диапазона посочен в условието. - В тялото на цикъла: oтпечатваме съобщение със съдържание "Invalid number!" на конзолата, след което присвояваме нова стойност за
numот входа на конзолата. - След като вече сме валидирали въведеното число, извън тялото на цикъла отпечатваме стойността на числото.
Ето и примерна реализация на алгоритъма чрез while цикъл:

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#5.
Най-голям общ делител (НОД)
Преди да продължим към следващата задача, е необходимо да се запознаем с определението за най-голям общ делител (НОД).
Определение за НОД: най-голям общ делител на две естествени числа a и b е най-голямото число, което дели едновременно и a, и b без остатък. Например:
| a | b | НОД |
|---|---|---|
| 24 | 16 | 8 |
| 67 | 18 | 1 |
| 12 | 24 | 12 |
| 15 | 9 | 3 |
| 10 | 10 | 10 |
| 100 | 88 | 4 |
Алгоритъм на Евклид
В следващата задача ще използваме един от първите публикувани алгоритми за намиране на НОД - алгоритъм на Евклид:
Докато не достигнем остатък 0:
- Делим по-голямото число на по-малкото.
- Вземаме остатъка от делението.
Псевдо-код за алгоритъма на Евклид:
while b ≠ 0
var oldB = b;
b = a % b;
a = oldB;
print а;
Пример: най-голям общ делител (НОД)
Да се въведат цели числа a и b и да се намери НОД(a, b).
Ще решим задачата чрез алгоритъма на Евклид:
- Създаваме променливи
aиb, на които присвояваме целочислени стойности, взети от входа на конзолата. - За условие на цикъла слагаме израз, който е
true, ако числотоbе различно от 0. - В тялото на цикъла следваме указанията от псевдо кода:
- Създаваме временна променлива, на която присвояваме текущата стойност на
b. - Присвояваме нова стойност на
b, която е остатъка от делението наaиb. - На променливата
aприсвояваме предишната стойност на променливатаb.
- Създаваме временна променлива, на която присвояваме текущата стойност на
- След като цикълът приключи и сме установили НОД, го отпечатваме на екрана.

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#6.
Do-while цикъл
Следващият цикъл, с който ще се запознаем, е do-while, в превод - прави-докато. По структура, той наподобява while, но има съществена разлика между тях. Тя се състои в това, че do-while ще изпълни тялото си поне веднъж. Защо се случва това? В конструкцията на do-while цикъла, условието винаги се проверява след тялото му, което от своя страна гарантира, че при първото завъртане на цикъла, кодът ще се изпълни, а проверката за край на цикъл ще се прилага върху всяка следваща итерация на do-while.
Следва обичайната поредица от примерни задачи, чиито решения ще ни помогнат да разберем по-добре do-while цикъла.
Пример: изчисляване на факториел
За естествено число n да се изчисли n! = 1 * 2 * 3 * … * n. Например, ако n = 5, то резултатът ще бъде: 5! = 1 * 2 * 3 * 4 * 5 = 120.
Ето как по-конкретно можем да пресметнем факториел:
- Създаваме променливата
n, на която присвояваме целочислена стойност взета от входа на конзолата. - Създаваме още една променлива -
fact, чиято начална стойност е 1. Нея ще използваме за изчислението и съхранението на факториела. - За условие на цикъла ще използваме
n > 1, тъй като всеки път, когато извършим изчисленията в тялото на цикъла, ще намаляваме стойността наnс 1. - В тялото на цикъла:
- Присвояваме нова стойност на
fact, която е резултат от умножението на текущата стойност наfactс текущата стойност наn. - Намаляваме стойността на
nс -1.
- Присвояваме нова стойност на
- Извън тялото на цикъла отпечатваме крайната стойност на факториела.

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#7.
Пример: сумиране на цифрите на число
Да се сумират цифрите на цяло положително число n. Например, ако n = 5634, то резултатът ще бъде: 5 + 6 + 3 + 4 = 18.
Можем да използваме следната идея, за да решим задачата:
- Създаваме променливата
n, на която присвояваме стойност, равна на въведеното от потребителя число. - Създаваме втора променлива -
sum, чиято начална стойност е 0. Нея ще използваме за изчислението и съхранението на резултата. - За условие на цикъла ще използваме
n > 0, тъй като след всяко изчисление на резултата в тялото на цикъла, ще премахваме последната цифра отn. - В тялото на цикъла:
- Присвояваме нова стойност на
sum, която е резултат от събирането на текущата стойност наsumс последната цифра наn. - Присвояваме нова стойност на
n, която е резултат от премахването на последната цифра отn.
- Присвояваме нова стойност на
- Извън тялото на цикъла отпечатваме крайната стойност на сумата.

n % 10: връща последната цифра на числото n.n / 10: изтрива последната цифра на n. |
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#8.
Безкрайни цикли и операторът break
До момента се запознахме с различни видове цикли, като научихме какви конструкции имат те и как се прилагат. Следва да разберем какво е безкраен цикъл, кога възниква и как можем да прекъснем изпълнението му чрез оператора break.
Безкраен цикъл. Що е то?
Безкраен цикъл наричаме този цикъл, който повтаря безкрайно изпълнението на тялото си. При while и do-while циклите проверката за край е условен израз, който винаги връща true. Безкраен for възниква, когато липсва условие за край.
Ето как изглежда безкраен while цикъл:

А така изглежда безкраен for цикъл:

Оператор break
Вече знаем, че безкрайният цикъл изпълнява определен код до безкрайност, но какво става, ако желаем в определен момент при дадено условие, да излезем принудително от цикъла? На помощ идва операторът break, в превод - спри, прекъсни.
Операторът break спира изпълнението на цикъла към момента, в който е извикан, и продължава от първия ред след края на цикъла. Това означава, че текущата итерация на цикъла няма да бъде завършена до край и съответно останалата част от кода в тялото на цикъла няма да се изпълни. |
Пример: прости числа
В следващата задача се изисква да направим проверка за просто число. Преди да продължим към нея, нека си припомним какво са простите числа.
Определение: едно цяло число е просто, ако се дели без остатък единствено на себе си и на 1. По дефиниция простите числа са положителни и по-големи от 1. Най-малкото просто число е 2.
Можем да приемем, че цяло число n е просто, ако n > 1 и n не се дели на число между 2 и n-1.
Първите няколко прости числа са: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, …
За разлика от тях, непростите (композитни) числа са такива числа, чиято композиция е съставена от произведение на прости числа.
Ето няколко примерни непрости числа:
- 10 = 2 * 5
- 42 = 2 3 7
- 143 = 13 * 11
Алгоритъм за проверка дали дадено цяло число е просто: проверяваме дали n > 1 и n се дели на 2, 3, …, n-1 без остатък.
- Ако се раздели на някое от числата, значи е композитно.
- Ако не се раздели на никое от числата, значи е просто.
Можем да оптимизираме алгоритъма, като вместо проверката да е до n-1, да се проверяват делителите до √n. Помислете защо. |
Пример: проверка за просто число. Оператор break
Да се провери дали едно число n е просто. Това ще направим като проверим дали n се дели на числата между 2 и √n.
Ето го алгоритъмът за проверка за просто число, разписан постъпково:
- Създаваме променливата
n, на която присвояваме цяло число въведено от входа на конзолата. - Създаваме булева променлива
isPrimeс начална стойностtrue, ако числото е по-голямо или равно на две (защото по дефиниция числа като 0, 1, -1 и -2 не са прости). Приемаме, че едно число е просто до доказване на противното. - Създаваме
forцикъл, на който като начална стойност за променливата на цикъла задаваме 2, за условие текущата ѝ стойност<= √n. Стъпката на цикъла е 1. - В тялото на цикъла проверяваме дали
n, разделено на текущата стойност има остатък. Ако от делението няма остатък, то променямеisPrimeнаfalseи излизаме принудително от цикъла чрез операторbreak. - В зависимост от стойността на
isPrimeотпечатваме дали числото е просто (true) или съответно съставно (false).
Ето и примерна имплементация на описания алгоритъм:

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#9.
Пример: оператор break в безкраен цикъл
Да се напише програма, която проверява дали едно число n е четно, и ако е - да се отпечатва на екрана. За четно считаме число, което се дели на 2 без остатък. При невалидно число да се връща към повторно въвеждане и да се изписва съобщение, което известява, че въведеното число не е четно.
Ето една идея как можем да решим задачата:
- Създаваме променлива
n, на която присвояваме начална стойност 0. - Създаваме безкраен
whileцикъл, като за условие ще зададемtrue. - В тялото на цикъла:
- Вземаме целочислена стойност от входа на конзолата и я присвояваме на
n. - Ако числото е четно, излизаме от цикъла чрез
break. - В противен случай извеждаме съобщение, което гласи, че числото не е четно. Итерациите продължават, докато не се въведе четно число.
- Вземаме целочислена стойност от входа на конзолата и я присвояваме на
- Отпечатваме четното число на екрана.
Ето и примерна имплементация на идеята:

Забележка: макар кодът по-горе да е коректен, той няма да работи, ако вместо числа потребителят въведе текст, например “Invalid number”. Тогава парсването на текста към число ще се счупи и програмата ще покаже съобщение за грешка (изключение). Как да се справим с този проблем и как да прихващаме и обработваме изключения чрез try-catch конструкцията ще научим след малко.
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#10.
Вложени цикли и операторът break
След като вече научихме какво са вложените цикли и как работи операторът break, е време да разберем как работят двете заедно. За по-добро разбиране, нека стъпка по стъпка да напишем програма, която трябва да направи всички възможни комбинации от двойки числа. Първото число от комбинацията е нарастващо от 1 до 3, а второто е намаляващо от 3 до 1. Задачата трябва да продължи изпълнението си, докато i + j не е равно на 2 (т.е. i = 1 и j = 1).
Желаният резултат е:

Ето едно грешно решение, което изглежда правилно на пръв поглед:

Ако оставим програмата ни по този начин, резултатът ни ще е следният:
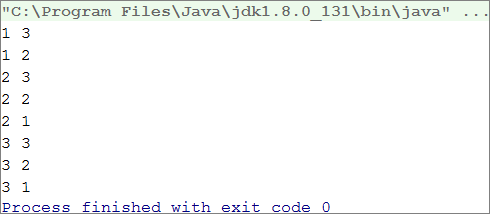
Защо се получава така? Както виждаме, в резултата липсва "1 1". Когато програмата стига до там, че i = 1 и j = 1, тя влиза в if проверката и изпълнява break операцията. По този начин се излиза от вътрешния цикъл, но след това продължава изпълнението на външния. i нараства, програмата влиза във вътрешния цикъл и принтира резултата.
Когато във вложен цикъл използваме оператора break, той прекъсва изпълнението само на вътрешния цикъл. |
Какво е правилното решение? Един начин за решаването на този проблем е чрез деклариране на bool променлива, която следи за това, дали трябва да продължава въртенето на цикъла. При нужда от изход (излизане от всички вложени цикли), се прави true променливата и се излиза от вътрешния цикъл с break, а при последваща проверка се напуска и външния цикъл. Ето и примерна имплементация на тази идея:
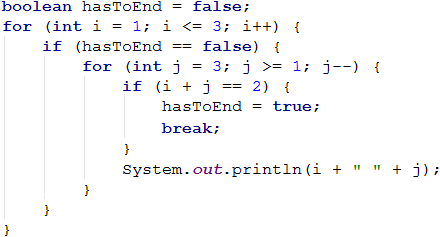
По този начин, когато i + j = 2, програмата ще направи променливата hasToEnd = true и ще излезе от вътрешния цикъл. При следващото завъртане на външния цикъл, чрез if проверката, програмата няма да може да стигне до вътрешния цикъл и ще прекъсне изпълнението си.
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#11.
Справяне с грешни данни: try-catch
Последното, с което ще се запознаем в тази глава, е как да "улавяме" грешни данни чрез конструкцията try-catch.
Какво е try-catch?
Програмната конструкция try-catch служи за прихващане и обработка на изключения (грешки) по време на изпълнението на програмата.
В програмирането изключенията представляват уведомление за дадено събитие, което нарушава нормалната работа на една програма. Такива изключителни събития прекъсват изпълнението на програмата ни и тя търси кой да обработи настъпилата ситуация. Ако не намери, изключението се отпечатва на конзолата (програмата “гърми”). Ако намери, изключението се обработва и програмата продължава нормалното си изпълнение без да “гърми”. След малко ще видим как точно става това.
Когато настъпи изключение, се казва, че изключението е било "хвърлено" (throw exception). От там идва и изразът "улавям изключение" (catch exception).
Конструкция на try-catch
Конструкцията try-catch има различни варианти, но за сега ще се запознаем само с най-основния от тях, при който catch блокът ще прихване всяка грешка в променлива с име ex:

В следващата задача ще видим нагледно, как да се справим в ситуация, в която потребителят въвежда вход, различен от число (например string вместо int), чрез try-catch.
Пример: справяне с грешни числа чрез try-catch
Да се напише програма, която проверява дали едно число n е четно и ако е, да се отпечатва на екрана. При невалидно въведено число да се изписва съобщение, че въведения вход не е валидно число и въвеждането да продължи отново.
Ето как можем да решим задачата:
- Създаваме безкраен
whileцикъл, като за условие ще зададемtrue. - В тялото на цикъла:
- Създаваме
try-catchконструкция. - В
tryблока пишем програмната логика за четене на потребителския вход, парсването му до число и проверката за четност. - При четно число го отпечатваме и излизаме от цикъла (с
break). Програмата си е свършила работата и приключва. - При нечетно число отпечатваме съобщение, че се изисква четно число, без да излизаме от цикъла (защото искаме той да се повтори отново).
- Ако хванем изключение при изпълнението на
tryблока, изписваме съобщение за невалидно въведено число (и цикълът съответно се повтаря, защото не излизаме изрично от него).
- Създаваме
Ето и примерна имплементация на описаната идея:
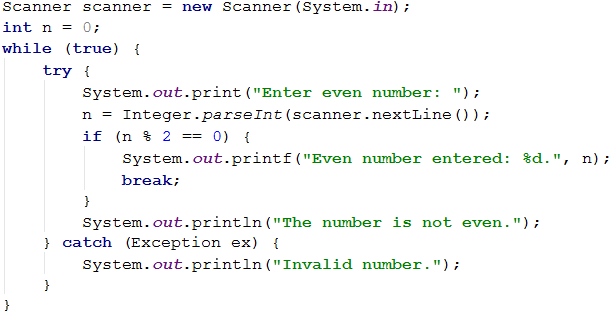
Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#12.
Сега вече решението трябва да работи винаги: независимо дали въвеждаме цели числа, невалидни числа (например твърде много цифри) или текстове, които не съдържат числа.
Задачи с цикли
В тази глава се запознахме с няколко нови вида цикли, с които могат да се правят повторения с по-сложна програмна логика. Да решим няколко задачи, използвайки новите знания.
Задача: числа на Фибоначи
Числата на Фибоначи в математиката образуват редица, която изглежда по следния начин: 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Формулата за образуване на редицата е:
F0 = 1
F1 = 1
Fn = Fn-1 + Fn-2
Примерен вход и изход
| Вход (n) | Изход | Коментар |
|---|---|---|
| 10 | 89 | F(11) = F(9) + F(8) |
| 5 | 8 | F(5) = F(4) + F(3) |
| 20 | 10946 | F(20) = F(19) + F(18) |
| 0 | 1 | |
| 1 | 1 |
Да се въведе цяло число n и да се пресметне n-тото число на Фибоначи.
Насоки и подсказки
Идея за решаване на задачата:
- Създаваме променлива
n, на която присвояваме целочислена стойност от входа на конзолата. - Създаваме променливите
f0иf1, на които присвояваме стойност 1, тъй като така започва редицата. - Създаваме
forцикъл с условие текущата стойностi < n - 1. - В тялото на цикъла:
- Създаваме временна променлива
fNext, на която присвояваме следващото число в поредицата на Фибоначи. - На
f0присвояваме текущата стойност наf1. - На
f1присвояваме стойността на временната променливаfNext.
- Създаваме временна променлива
- Извън цикъла отпечатваме числото n-тото число на Фибоначи.
Примерна имплементация:

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#13.
Задача: пирамида от числа
Да се отпечатат числата 1 … n в пирамида като в примерите по долу. На първия ред печатаме едно число, на втория ред печатаме две числа, на третия ред печатаме три числа и т.н. докато числата свършат. На последния ред печатаме толкова числа, колкото останат докато стигнем до n.
Примерен вход и изход
| Вход | Изход | Вход | Изход | Вход | Изход |
|---|---|---|---|---|---|
| 7 | 1 2 3 4 5 6 7 |
5 | 1 2 3 4 5 |
10 | 1 2 3 4 5 6 7 8 9 10 |
Насоки и подсказки
Можем да решим задачата с два вложени цикъла (по редове и колони) с печатане в тях и излизане при достигане на последното число. Ето идеята, разписана по-подробно:
- Създаваме променлива
n, на която присвояваме целочислена стойност от входа на конзолата. - Създаваме променлива
numс начална стойност 1. Тя ще пази броя на отпечатаните числа. При всяка итерация ще я увеличаваме с 1 и ще я принтираме. - Създаваме външен
forцикъл, който ще отговаря за редовете в таблицата. Наименуваме променливата на цикълаrowи ѝ задаваме начална стойност 0. За условие слагамеrow < n. Размерът на стъпката е 1. - В тялото на цикъла създаваме вътрешен
forцикъл, който ще отговаря за колоните в таблицата. Наименуваме променливата на цикълаcolи ѝ задаваме начална стойност 0. За условие слагамеcol < row(row= брой цифри на ред). Размерът на стъпката е 1. - В тялото на вложения цикъл:
- Проверяваме дали
col > 1, ако да – принтираме разстояние. Ако не направим тази проверка, а директно принтираме разстоянието, ще имаме ненужно такова в началото на всеки ред. - Отпечатваме числото
numв текущата клетка на таблицата и го увеличаваме с 1. - Правим проверка за
num > n. Акоnumе по-голямо отn, прекъсваме въртенето на вътрешния цикъл.
- Проверяваме дали
- Отпечатваме празен ред, за да преминем на следващия.
- Отново проверяваме дали
num > n. Ако е по-голямо, прекъсваме изпълнението на програмата ни чрезbreak.
Ето и примерна имплементация:

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#14.
Задача: таблица с числа
Да се отпечатат числата 1 … n в таблица като в примерите по-долу.
Примерен вход и изход
| Вход | Изход | Вход | Изход |
|---|---|---|---|
| 3 | 1 2 3 2 3 2 3 2 1 |
4 | 1 2 3 4 2 3 4 3 3 4 3 2 4 3 2 1 |
Насоки и подсказки
Можем да решим задачата с два вложени цикъла и малко изчисления в тях:
- Четем от конзолата размера на таблицата в целочислена променлива
n. - Създаваме
forцикъл, който ще отговаря за редовете в таблицата. Наименуваме променливата на цикълаrowи ѝ задаваме начална стойност 0. За условие слагамеrow < n. Размерът на стъпката е 1. - В тялото на цикъла създаваме вложен
forцикъл, който ще отговаря за колоните в таблицата. Наименуваме променливата на цикълаcolи ѝ задаваме начална стойност 0. За условие слагамеcol < n. Размерът на стъпката е 1. - В тялото на вложения цикъл:
- Създаваме променлива
num, на която присвояваме резултата от текущият ред + текущата колона + 1 (+1, тъй като започваме броенето от 0). - Правим проверка за
num > n. Акоnumе по-голямо от n, присвояваме нова стойност наnumравна на два пъти n - текущата стойност заnum. Това правим с цел да не превишавамеnв никоя от клетките на таблицата.- Отпечатваме числото от текущата клетка на таблицата.
- Създаваме променлива
- Отпечатваме празен ред във външния цикъл, за да преминем на следващия ред.

Тестване в Judge системата
Тествайте решението си тук: https://judge.softuni.org/Contests/Practice/Index/659#15.
Какво научихме от тази глава?
Можем да използваме for цикли със стъпка:
for (int i = 1; i <= n; i+=3) {
System.out.println(i);
}
Циклите while / do-while се повтарят докато е в сила дадено условие:
int num = 1;
while (num <= n) {
System.out.println(num++);
}
Ако се наложи да прекъснем изпълнението на цикъл, го правим с оператора break:
int n = 0;
while (true) {
n = Integer.parseInt(scanner.nextLine());
if (n % 2 == 0) {
break; // even number -> exit from the loop
}
System.out.println("The number is not even.");
}
System.out.println("Even number entered: {0}", n);
Вече знаем как да прихващаме грешки по време на изпълнението на програмата ни:
try {
System.out.println("Enter even number: ");
int n = Integer.parseInt(scanner.nextLine());
} catch (Exception ex) {
System.out.println("Invalid number.");
}
// Ако Integer.parseInt(…) гръмне, ще се изпълни catch { … } блокът